Vectorul X ≠ 0 se numește un vector propriu al operatorului liniar cu matricea A, în cazul în care există un număr de l, că AX = Lx.
Numărul l numit eigenvalue (matricea A) ce corespunde vectorului X.
Cu alte cuvinte, vectorul propriu - este un vector care sub acțiunea unui operator liniar intră vector coliniare, adică, pur și simplu, înmulțit cu un numar. În contrast, vectorii necorespunzătoare transforma mai dificilă.
Scriem propria dvs. definiție a unui vector sub forma unui sistem de ecuații:
Se transferă toate condițiile de pe partea stângă:
putem scrie ultimul sistem în formă de matrice, după cum urmează:
Sistemul rezultat este întotdeauna soluție zero, X = O. Astfel de sisteme, în care toți termenii constante sunt zero, numit omogen. Dacă matricea sistemului - un pătrat, iar determinantul său nu este zero, atunci de regula lui Cramer, vom obține întotdeauna o soluție unică - zero. Se poate demonstra că sistemul are soluții netriviale dacă și numai dacă determinantul acestei matrice este egal cu zero, adică,
Această ecuație cu l necunoscută numită ecuație caracteristică (polinomul caracteristic) a matricei A (operatorul liniar).
Se poate demonstra că polinomul caracteristic al unui operator liniar este independentă de alegerea temei.
De exemplu, găsim vectori și valori proprii ale unui operator liniar definit de matricea A =.
Pentru a face acest lucru, compune ecuația caracteristică | A - LE | = (1 - l) 2 - R36 = 1 - 2l + l 2 - R36 = l 2 - 2l - 35 = 0; A = 4 + 140 = 144; l1 = valori proprii (2 - 12) / 2 = -5; l2 = (2 + 12) / 2 = 7.
Pentru a găsi vectorii proprii, de rezolvare a două sisteme de ecuații
Pentru prima dintre aceste matrice augmented are forma
,
Pentru a doua matrice una extins ia forma
,
cu eigenvalue (-5) și toți vectorii de forma ((2/3) c1, c1) cu 7 eigenvalue - (C (2/3)) Astfel, vectorii proprii ale acestui operator liniar sunt toate speciile de vectori.
Se poate demonstra că matricea operatorului A în baza constând din vectori proprii săi este diagonală și are forma:
,
unde li - autovalorile acestei matrice.
Invers, dacă matricea A într-o bază este diagonală, toți vectorii din această bază vor fi vectorii proprii ale acestei matrici.
Este de asemenea posibil să se arate că, în cazul în care operatorul liniar are valori proprii distincte n, vectorii proprii corespunzătoare sunt liniar independente, iar matricea operatorului în baza corespunzătoare este diagonală.
Vom explica acest lucru în exemplul anterior. Ia valori arbitrare nenule și C1. dar astfel încât vectorii X (1) și X (2) sunt liniar independente, adică au format baza. De exemplu, să presupunem că c = c1 = 3, atunci X (1) = (-2, 3), X (2) = (2, 3). Să verifice independența liniară a vectorilor:
= -12 ≠ 0. În această nouă matrice bază A are forma A * =.
Pentru a verifica acest lucru, folosim formula A = C -1 * AS. În primul rând, vom găsi C -1.
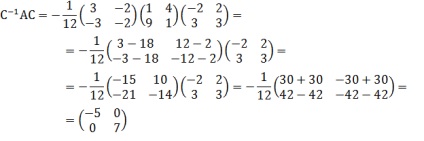
formă pătratică f (.. X1 x2 xn) de n variabile se numește suma pe care fiecare membru al care este un pătrat de una dintre variabilele sau produsul a două variabile diferite, realizate cu unele coeficient: f (.. X1 x2 xn) = (aij = aji ).
O matrice compusă din acești coeficienți, se numește formă pătratică matrice. Este întotdeauna o matrice simetrică (adică matricea, simetrică față de diagonala principală, aij = aji).
Notația matrice, forma pătratică f (X) = X T AX, unde
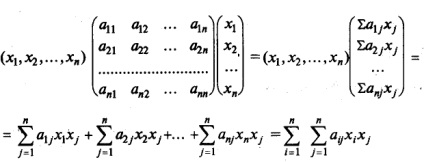
De exemplu, o formă pătratică, se scrie în formă de matrice.
Pentru a face acest lucru, vom găsi matricea formei pătratice. Elementele sale diagonale sunt egale cu pătratelor coeficienților variabilelor, și alte elemente - Jumătate dintre coeficienții corespunzători ai formei pătratice. prin urmare
Să variabilă matrice coloană X obținută nedegenerat matricea de transformare liniară coloană-Y, adică, X = CY, unde C - nesingular ordine n-lea. Apoi, forma pătratică
f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.
Astfel, atunci când transformarea liniară nedegenerata cu matricea formei pătratice are forma: A * = C T AC.
De exemplu, găsim o formă pătratică f (y1 y2.), Derivat din forma pătratică f = 2x1 2 4x1 + x2 (x1, x2). - 3x2 transformare 2 liniar.
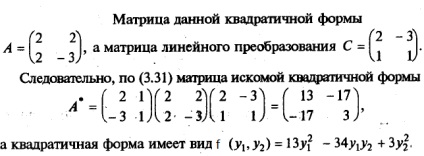
Forma pătratică numită canonic (are forma canonică), în cazul în care toți coeficienții ij = 0 pentru i ≠ j, adică
f (x1. x2. xn) = a11 x1 + a22 x2 2 2 + ... + ann xn = 2.
matricea sa este diagonală.
Teorema (dovada nu este dat aici). Orice formă pătratică poate fi redus la forma canonică utilizând o transformare liniară non-degenerate.
Pentru a face acest lucru, selectați mai întâi un pătrat perfect de x1 variabila:
Acum selectați un pătrat perfect de x2 variabile:
Rețineți că o formă canonică a unei forme pătratice unic definită (una și aceeași formă pătratică poate fi redus pentru a forma diferite metode canonice [1]). Cu toate acestea obținute în diferite moduri, forme canonice au o serie de proprietăți comune. În special, numărul de termeni cu formă pozitivă (negativă) a coeficienților pătratice nu depinde de metoda de reducere pentru a forma acest tip (de exemplu, în exemplul va fi întotdeauna două negative și un coeficient pozitiv). Această proprietate este numit legea de inerție a formelor pătratice.
De asemenea, trebuie remarcat faptul că gradul de forma pătratică este numit rangul de forma pătratică. egal cu numărul de factori de formă canonică nenule și nu se modifică sub transformări liniare.
Formularul pătratice f (X) este numit pozitiv (negativ) definit. în cazul în care toate valorile variabilelor care nu sunt egale cu zero în același timp, este pozitiv, adică, f (X)> 0 (negativ, adică
f (X) <0).
De exemplu, forma pătratică f1 (X) = x1 + x2 2 2 - definit pozitiv, deoarece reprezintă suma pătratelor și o formă pătratică f2 (X) = -X1 2 x2 + 2x1 - x2 2 - definit negativ, deoarece reprezintă poate fi reprezentat ca f2 (X) = - (x1 - x2) 2.
În cele mai multe situații practice pentru a stabili un semn clar al formei pătratice este ceva mai complicat, așa că pentru această utilizare una dintre următoarele teoreme (le-am stat fără dovezi).
Teorema. Forma pătratică este pozitiv (negativ) definit dacă și numai dacă toate valorile proprii sale sunt matrice pozitiv (negativ).
Teorema (criteriul Sylvester). Forma pătratică este pozitiv definită dacă și numai dacă toate principalele minori ale acestei forme sunt pozitive.
Main (unghiular) minor ordin k al matricei A ordinul n-lea se numește determinantul matricei constând din primele rânduri k și coloanele A ().
Rețineți că pentru o formă pătratică negativ definit semnalizările minori principali sunt alternate, primul ordin minor trebuie să fie negativ.
De exemplu, pentru a examina semn fix pătratice formă f (x1. X2) = 2x1 + 4x1 2 3x2 + x2 2.
Metoda 1: construirea unei matrice pătratică A = formular. Ecuația caracteristică va avea forma = (2 - l) *
* (3l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25-8 = 17;
. Prin urmare, forma pătratică - definită pozitiv.
Metoda 2. Main Minor de ordinul întâi a A D1 = a11 = 2> 0. principal al doilea ordin minor D2 = = 6 - 2 = 4> 0. Prin urmare, criteriul Sylvester forma pătratică - pozitiv definită.
Investigați la un alt semn definit formă pătratică, f = -2x1 + 4x1 2 x2 (x1, x2). - 3x2 2.
Metoda 1: construirea unei matrice pătratică A = formular. Ecuația caracteristică va avea forma = (-2 - l) *
* (- 3l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25-8 = 17;
. Prin urmare, forma pătratică - definit negativ.
Metoda 2. Main Minor de ordinul întâi a A D1 = a11 =
= -2 <0. Главный минор второго порядка D2 = = 6 – 4 = 2> 0. Prin urmare, criteriul Sylvester forma pătratică - negativi definite (principalii minori semne alternative variind de la minus).
Și, ca un alt exemplu, să examineze la fix semn pătratice formă f = 2x1 2 4x1 + x2 (x1, x2). - 3x2 2.
Metoda 1: construirea unei matrice pătratică A = formular. Ecuația caracteristică va avea forma = (2 - l) *
* (- 3l) - 4 = (-6 - 2l + 3l + l 2) - 4 2 = l + l - 10 = 0; D = 1 + 40 = 41;
. Unul dintre aceste numere este negativ, iar celălalt - pozitiv. Semne de valori proprii diferite. Prin urmare, forma pătratică nu poate fi nici negativ, nici pozitiv definită, și anume, Această formă pătrată nu este certă (poate lua valori de fiecare semn).
Metoda 2. Main Minor de ordinul întâi a A D1 = a11 = 2> 0. principal al doilea ordin minor D2 = = -6-4 = -10 <0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).