Pentru cercetătorul este important să se cunoască acuratețea și fiabilitatea evaluării fiecărui cadru special, care dă o idee despre intervalele de încredere.
Un interval de încredere unilateral este numit un interval de la X # 949; la parametrul necunoscut sau parametrul necunoscut X + # 949;, care stabilește fie limita inferioară sau superioară a unui parametru necunoscut, cu un nivel de încredere predeterminat de Pd.
interval de încredere bilateral se numește un interval de la X # 949; până la X + # 949;, care acoperă un parametru de distribuție necunoscută cu Pd probabilitate de încredere predeterminată.
eroare de încredere # 949; Acesta caracterizează parametrul de distribuție de eroare aleatoare. Mai mică valoare # 949; mai mare acuratețea estimării H.
Încrederea probabilitate Pd sau fiabilitatea corespunzătoare acestui interval de încredere se numește probabilitatea ca valoare reală X multor caracteristici numerice se află în acest interval.
Cantitate egală cu a = 1 - Pg se numește nivel de semnificație și este, uneori, exprimată în%. Se caracterizează probabilitatea de evenimente, condiționat acceptate pentru incredibil.
Pentru a controla calitatea produsului probabilitatea de încredere Pd este luată egală cu 0.95-0.99.
Intervalul de încredere este limitat la limitele de încredere inferioare și superioare, în cadrul acesteia cu o anumită probabilitate este caracteristica sumară.
Intervale de încredere pentru valoarea medie.
Pentru frontieră pe o singură parte:
Limita inferioara (12)
Limita superioară (13)
limite bilaterale:
Limita inferioara (14)
Limita superioară (15)
unde t1 și t - cuantila a distribuției Student la încredere g = 0,95, care valorile sunt prezentate în Tabelul 3.
În Excel, intervalele de încredere sunt calculate utilizând funcția INCREDERE (Fig. 17). Se returnează o valoare care poate fi utilizată pentru a determina intervalul de încredere pentru așteptările populației generale. Intervalul de încredere este intervalul de valori. Proba medie x este punctul de mijloc al acestui interval, atunci intervalul de încredere este definit ca (x ± CONFIDENCE).
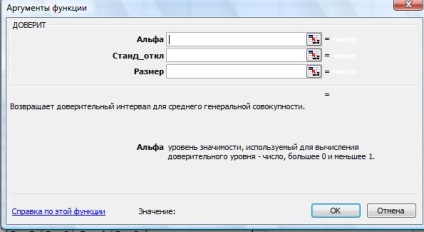
Fig. Funcția 17. CONFIDENCE
Alpha - un nivel de semnificație utilizat pentru a calcula nivelul de fiabilitate. Nivelul de fiabilitate este (1 - alfa). 100%, sau cu alte cuvinte, un alfa de 0.05 indică un nivel de 95 la suta de fiabilitate.
Stand_otkl - o deviație standard (abaterea medie pătrată) din populația generală pentru spațiul de date, se presupune a fi cunoscut.
Dimensiunea - este mărimea eșantionului.
Dacă nici un argument nu este numeric, CONFIDENCE returnează eroare #VALUE!.
În cazul în care alfa ≤ 0 sau alfa ≥ 1, încrederea funcția returnează valoarea de eroare # NUM!
Dacă stand_otkl ≤ 0, funcția CONFIDENCE returnează valoarea de eroare # NUM!.
Dacă dimensiunea nu este un număr întreg, acesta este rotunjit.
În cazul în care dimensiunea <1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.
Intervale de încredere pentru abaterea medie.
sunt definite după cum urmează în cazul în care numărul de încercări n<100:
unde S - deviația standard.
Valorile Zl și Zv sunt determinate folosind tabelul 4.
În cazul în care numărul de teste K = n-1> 100 valori ZL și ZV sunt calculate prin formula:
unde U = t1 la n = ∞ - cuantila a distribuției Student la încredere Pd = 0,95.
Intervale de încredere pentru coeficientul de variație.
unde C - un coeficient de variație.
Valorile Kn și Ap sunt prezentate în Tabelul 4.