Momentul pornirii (), tensiunea pe condensator este zero (). După comutarea (comutatorul în poziția „1“), pe plăcile condensatorului se vor acumula încărcare. și anume există condensator proces de încărcare. Tensiunea la bornele condensatorului este proporțională cu taxa pe plăcile sale:
În timpul încărcării condensatorului într-un circuit de curent fluxuri:
În consecință, curentul de încărcare a condensatorului este proporțională cu viteza de variație a tensiunii pe plăcile condensatorului.
Să considerăm procesul de schimbare a tensiunii pe condensator și curentul în circuit în timpul încărcării condensatorului, adică, în perioada de la rândul său, până la încărcarea completă a condensatorului atunci când. care corespunde procesului tranzitoriu în circuit cu un element capacitiv.
Pentru a identifica natura schimbării de tensiune pe condensator și curentul în circuit. Formam ecuația în conformitate cu legea 2a Kirchhoff (Figura 1 b):
Substituind valoarea curentă (2) până la (3):
rezistență și capacitate produsului:
Se numește lanț continuu de timp și se măsoară în secunde. apoi:
Separarea variabilelor, obținem:
Expresia (5) este o ecuație diferențială, a cărei soluție este:
Această ecuație arată că tensiunea la bornele condensatorului variază exponențial (în creștere exponent). Teoretic condensator (Fig.2) procesul de încărcare durează la nesfârșit, deoarece tensiunea condensatorului va fi egală numai în cazul în care. Practic, procesul de încărcare este finalizat prin (4-5).
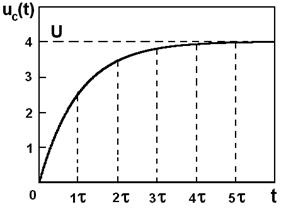
Din moment. ce mai mult și. mai lent procesul condensator de încărcare.
Din ecuația (3) putem obține o expresie pentru curentul în circuit:
ceea ce implică faptul că:
Din ecuația (8) rezultă că curentul în circuit variază într-o exponențială descrescătoare având un maxim în momentul energizare, de vreme. și după încărcarea condensatorului cu (Fig. 3).
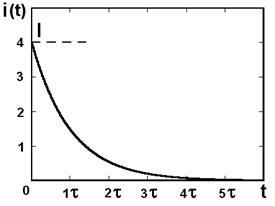
II. descărcare condensator proces
Să considerăm circuitul când comutatorul de la poziția „1“ este setat la „2“. condensator taxa plăci începe să scadă, curentul în circuitul va fi și, prin urmare, condensatorul se va descărca. Curentul din circuit este determinat de rata de degradare a taxei pe plăcile condensatorului (așa cum este indicat prin semnul „-“).:
Al 2-lea drept Kirchhoff:
Rezolvarea ecuației diferențiale (10), obținem:
Din moment. și apoi, în cele din urmă:
Expresiile (11) și (12) arată că o scădere exponențială.
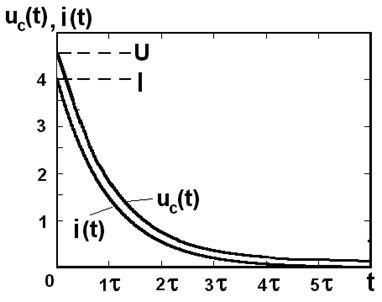
Fig. 4 prezintă tensiune și curent prin condensator în timpul descărcării acestuia.