Găsiți limitele specificate:
a) prin înlocuirea variabilei a valorii sale limită de 2 obține
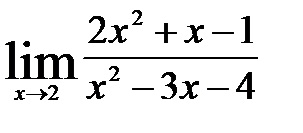
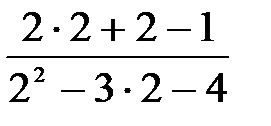
b) Înlocuind aceasta pentru valoarea limită variabilă -1 este obținută sub formă nedeterminată.
Pentru eliminarea acestui tip de incertitudine în acest caz reprezintă polinomului pătratic numărătorul și numitorul ca produs al multiplicatorilor liniare utilizând cunoscuta formula:
unde - rădăcinile polinomului pătratic
.
Noi. ca polinomul pătratică discriminantă
Acum, un exemplu de condiție poate fi rescrisă într-o formă diferită și extinde soluția:
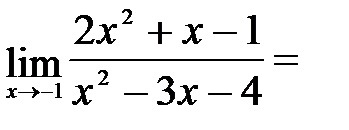
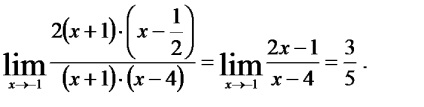
Aici ne confruntăm cu incertitudini. care poate scăpa de impunerea între paranteze în numărătorul și numitorul cel mai înalt grad sau numărătorul de pre-variabilă și numitorul fracției împărțit în. n cazul în care cel mai înalt grad de numărătorul și numitorul.
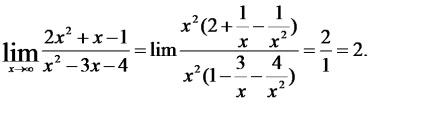
În primul caz, pentru scutirea de incertitudine, vom folosi prima limită remarcabilă și una dintre consecințele evidente:
Exemple de soluții vor fi după cum urmează:
În al doilea caz pentru scutirea de incertitudine, vom folosi doua limită remarcabilă și una dintre consecințele evidente:
Exemple de soluții vor fi după cum urmează:
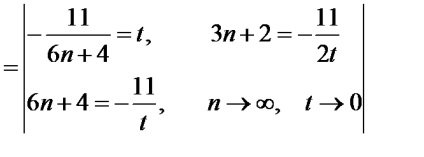
substituirea directă a valorii limită a rezultatelor argument într-un fel de incertitudine. , Multiply numărătorul și numitorul fracției să dezvăluie acest lucru la valoarea de incertitudine
Găsiți derivați. utilizând regulile și formulele de diferențiere. În abordarea tuturor următoarele exemple, în plus față de masă regulile bine cunoscute ale sumelor de diferentiere a derivaților sunt utilizați, diferența, produsul, împușcat, iar teorema derivata unei funcții compozit.
g) Dacă specificați o funcție complexă în cazul în care este, în cazul în care fiecare dintre funcțiile și se diferențiază în ceea ce privește argumentul său, atunci
Pentru a investiga functia de metode de calcul diferențial pentru a desena grafice lor. Studiul funcțiilor și grafice sunt recomandate după cum urmează:
1) Găsiți domeniul funcției
2) Pentru a investiga functia de continuitate; găsi un punct de discontinuitate a funcției și limitele sale unilaterale la punctele de discontinuitate;
3) găsiți funcția de punctul extremum și de a determina intervalele sale de monotonie;
4) găsi punctul de inflexiune al graficului și determină intervalele de convexitate și concavitate a graficului;
5) Găsiți asimptota graficului;
6) trage un grafic, folosind rezultatele studiilor anterioare;
7) pentru funcția de a găsi cele mai mari și cele mai mici valori în intervalul
1) Domeniul acestei funcții este de toate valorile reale ale argumentului care este, =. ceea ce înseamnă că funcția este continuă pe linia reală întreg și graficul ei nu are nici o asimptotă verticală.
2) studiază funcția extremum și intervalele de monotonie. În acest scop, vom găsi derivatul său și echivala cu zero:
. Rezolvarea ecuației pătratice obținute, putem concluziona că funcția are două puncte critice 1 sort: Divide domeniul acestor puncte pe părțile și derivații pentru a schimba semnul în ele dezvăluie perioadele de monotonie și prezența extremă.
3) definește punctul de inflexiune al graficului, intervalele de convexitate și concavitatea. Pentru a găsi derivata a doua a funcției date și setați-o egală cu zero:
; .
Astfel, funcția are un punct critic 2 natură
Noi împărțim domeniul punctului de primit din partea, fiecare dintre care stabilesc semnul derivatei a doua:
Valoarea abscisa punctului de inflexiune al funcției graficului, iar ordonata a acestui punct:
4) Să ne determina prezența graficului unei funcții date de pantă asimptota. Pentru a determina parametrii formulelor de utilizare ecuația asimptota:
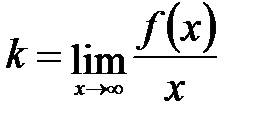
Astfel, graficul funcției dată nu este asimptote înclinată.
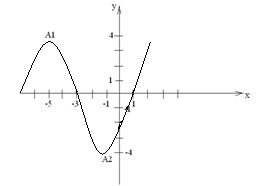
5) Pentru a reprezenta grafic sistemul de coordonate selectat reprezintă punctul maxim. minimă. inflexiune și grafică punctul de intersecție cu axa
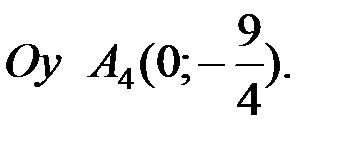
Luând în considerare rezultatele studiilor anterioare a stabili curba.
6) Găsiți cele mai mari și cele mai mici valori ale unei funcții date pe valorile COUNT intervalului pentru această funcție la capetele acestui segment, punctele critice de un fel prins pe segmentul și comparați rezultatele:
Explorați următoarea funcție și de a construi un grafic schematic:
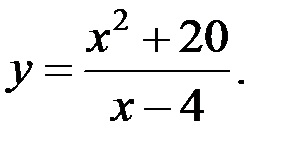
1) Domeniul de determinare:
2) Studiu privind continuitatea și punctele de discontinuitate clasificare.
Funcția Având în vedere este continuă pretutindeni, cu excepția la punctul. Calculăm limitele sale unilaterale asupra acestui punct:
Astfel, pentru un anumit punct, este o funcție de al doilea tip punctul de spargere, iar graficul linie verticală asimptota.
3) Studiul intervalelor extremum și monotonie.