Astăzi, vorbind despre statistici, voi discuta histograma. In general vorbind, histograma este o metodă de afișare grafică a grupării, adică distribuția setului de măsurători ale unor cantități de grupe, în conformitate cu o caracteristică esențială pentru acest grup. metode de grupare sunt utilizate pe scară largă pentru procesarea datelor brute.
În conformitate cu datele primare în statisticile înțelegem seriile statistice care sunt numite rânduri de difuzoare. dacă vorbim despre schimbarea fenomenului de timp, sau distribuirea de rânduri. atunci când este vorba despre compoziția sau structura fenomenului investigat.
Când este vorba despre rândurile care se bazează pe caracteristicile calitative (de exemplu, întreprinderea de proprietate), aceste serii sunt numite atributivă. în cazul în care seria construit de variabile (cum ar fi volumul cifrei de afaceri de risc), acestea sunt numite variațional.
În funcție de continuitatea de variație a variabilei distinge serii de variație discretă și intervalul.
O histogramă este un grafic bară construit din datele, care sunt împărțite în mai multe grupuri. Numărul de date care aparțin unui grup de fiecare (frecvență) este exprimată prin înălțimea coloanei corespunzătoare acestui grup.
Histograma poate fi construit pentru orice serie, în care, în cazul în care acesta este un atribut sau un număr de variație discrete (de exemplu, numărul de angajați din fiecare categorie tarifară), numărul de grupe alocate egal cu numărul de valori pentru acest atribut. În cazul unei serii ordonate de numărul de grupe interval va depinde de intervalul de valoare utilizată pentru gruparea datelor.
Interval - diferența dintre valorile maxime și minime ale atributului în fiecare grup. Este clar că mai mare, cu atât scade intervalul, și vice-versa. Grupul într-un astfel de caz este uneori menționată ca intervalele de clasă.
De exemplu, puteți rupe datele privind numărul de lucrători la următoarele grupuri de societăți:
până la 25 de persoane,
25-50 persoane
50-100 de persoane,
mai mult de 100 de persoane.
Apoi, histograma va conține 4 coloane, înălțimea, care va corespunde numărului de companii capturate în acest grup.
De altfel, observăm că cele de mai sus este un exemplu de distribuție de intervale inegale. dedicat, cum se spune, un program de cercetare, adică. e. de către noi înșine.
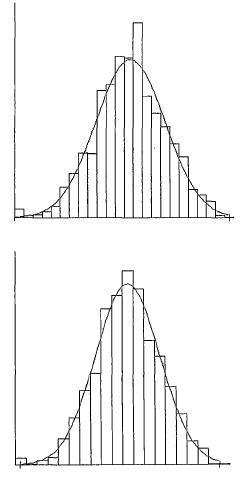
Q intervalul de selecție valoare (număr de grupuri) utilizate pentru a grupa elementele ordonate interval de serie, nu este inactiv. Pe lângă faptul că histograma este un mijloc excelent de vizualizare a datelor, acesta este, de asemenea, nu mai mult decât o aproximare a funcției de distribuție de probabilitate (a se vedea. Imaginea). E. Valoarea fiecărui grup de coloană prezintă probabilitatea ca valoarea următoare a măsurandului se încadrează în acest grup.
Prea multe grupuri pot da prea „jumpy“ program prea puțin - prea „buna“. În mod ideal, în mod evident, ar fi de dorit să aibă un număr de grupuri, care dă cea mai mică abatere de la funcția de distribuție de probabilitate, de ex., E. permite să dea estimarea cât mai exactă a acestei funcții de distribuție de probabilitate a fenomenului de studiu.
În general, acești matematicieni fac.
Primul, se pare, a fost Sterdzhesc (Sturges, 1926). El este considerat o histogramă de frecvență idealizată a claselor k, în cazul în care valoarea i-lea este egal cu coeficientul binomială. Pentru o formă suficient de mare k histograma se apropie de forma unei distribuții normale. Suma tuturor valorilor egale
.
Astfel, pentru n măsurători ale rezultatelor care se supune distribuția normală, numărul de clase utilizate în histograme trebuie luate ca forma histogramei obținută se va apropia de forma distribuției normale pentru un k suficient de mare. Aceasta este formula Sturgess. În această formă le-a luat aproape toate manualele pe statisticile.
Această formulă este acum criticat doar pentru faptul că utilizează în mod explicit distribuția binomială pentru a aproxima o distribuție normală, care nu este întotdeauna aplicabilă. Se crede că această formulă permite construirea unei histograme satisfăcătoare inclusiv cel puțin 200 măsurători.
Există o serie de formule alternative, unele dintre care lungimea calculată a intervalului, se determină apoi numărul de clase necesare (a se vedea. Aici).
Să considerăm o pereche de astfel de formule:
Formula Scott (Scott, 1979)
, unde h - lungimea intervalului, s - valori de deviație standard ale unui număr de măsurători
Formula diaconiță Friedman (Freedman și Diaconis, 1981)
, unde h - lungimea intervalului (IQ) - diferența dintre quartila superioară și inferioară.
Aceste formule sunt destul de simple și de sunet teoria statistică, și sunt considerate de preferat formula Sturgess.
În plus față de construirea unei histograme folosind numărul de clase obținute prin formula Sturgess, histograme sunt construite dintr-un număr de clase și Scott Friedman / Deaconess, precum și numărul de clase, utilizatorul stabilite arbitrar.
Desigur, aplicarea practică a acestui calculator, nu, dar puteți vedea diferența în numărul de clase și apariția histogramei.