Rezolvarea inegalităților polinomiale și raționale.
Vom folosi o combinație de metode algebrice și grafice pentru rezolvarea inegalităților polinomiale și raționale.
inegalitățile polinomiale
Ca o ecuație pătratică poate fi scris în forma AX 2 + bx + c = 0, inegalitatea trinom poate fi scrisă sub formă de ax 2 + bx + c. 0 unde. Poate. ≤ sau ≥. Iată câteva exemple de inegalități pătrat:
3x 2 - 2x - 5> 0, (-1/2) x 2 + 4x -7 ≤ 0.
Inegalitatea Square este un fel de inegalități polinomiale. Alte exemple de inegalități polinomiale:
-2x 4 + x 2 - 3 3 - 2x 2> 5x + 7.
Atunci când un simbol al inegalității în inegalității polinom înlocuiește cu forme semn de egalitate ecuație aferente. inegalitate Polinomial pot fi rezolvate cu ușurință, odată ce a decis ecuația legat.
EXEMPLUL 1 Solve: x 3 - x> 0.
Soluția de rezolvare Ni se cere să găsească toate valorile lui x, astfel încât x 3 - x> 0. Pentru a localiza aceste valori, vom trage funcția f (x) = x 3 -x. Apoi am observat că, atunci când funcția își schimbă semnul, graficul acesteia intersectează axa x. Deci, pentru a rezolva x 3 - x> 0, vom rezolva mai întâi ecuația asociată x 3 - x = 0 pentru a găsi toate zerouri:
x 3 - x = 0
x (x 2 - 1) = 0
x (x + 1) (x - 1) = 0.
Zeros este -1, 0 și 1. Astfel, punctul de intersecție cu axa x este (-1, 0), (0,0) și (1, 0), așa cum se arată mai jos. Zeros diviza axa x în patru intervale:
Pentru toate valorile lui x într-un marcaj interval predeterminat x 3 - x trebuie să fie pozitiv sau negativ. Dar, în scopul de a determina ce vom alege pentru a testa valoarea lui x în fiecare interval și pentru a găsi f (x). Noi putem determina semnul lui f (x) la fiecare interval, în ciuda graficul funcției.
Din moment ce am rezolvat x 3 - x> 0, setul de soluții include doar două dintre cele patru intervale în care semnul f (x) este pozitiv. Vedem că există soluții mnezhestvo (-1, 0), (1, ∞), sau.
Pentru a rezolva inegalitatea polinom:
1. Localizați inegalitatea echivalentă cu 0 pe o parte.
2. Decide ecuație polinomială asociată.
3. Utilizați decizia de a diviza axa x în intervale. Apoi selectați valoarea test de la fiecare interval și de a determina semnul polinomului în fiecare interval.
4. Se determină intervalele pentru care inegalitatea este adevărată și scrie interval de desemnare sau o multitudine de soluții. Inclusiv intervale end-point din setul de soluții, dacă o inegalitate caracter este ≤ sau ≥.
EXEMPLUL 2 Solve: 3x 4 + 10x ≤ 11x 3 + 4.
Prin scăderea deciziei 11x 3 + 4, vom forma inegalitatea echivalentă 3x 4 - 11x 3 + 10x - 4 ≤ 0.
soluție algebrică 4 - 11x 3 + 10x - 4 = 0,
. decizie
-1, 2, - √ 2. 2/3 și 2 + 2 √
sau despre
-1, 0586, 0667 și 3414.
Aceste numere sunt axa x este împărțit în cinci intervale:
(-∞, -1), (-1, 2 - √ 2), (2 - √ 2. 2/3), (2/3, 2 + √ 2) și (2 + √ 2. ∞).
Apoi, f (x) = 3x 4 - 11x 3 + 10x - și 4 și utilizând valorile de test pentru f (x), definim semnul f (x) la fiecare interval:
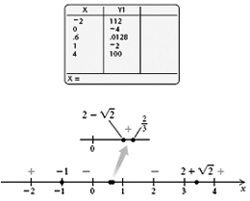
Valorile negative ale funcției la intervale (1, 2 - √ 2) și (2/3, 2 + √ 2). Deoarece semnul inegalității este ≤, includem punctele finale ale intervalelor din setul de soluții. Multe soluții au
[1, 2 - √ 2] [2/3, 2 + √ 2], sau.
Egal Funcția y = 3x 4 - 11x 3 + 10x - 4.
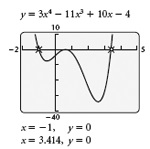
Vedem că există două zerouri la punctele 1 și aproximativ 3.414 (2 + 2 √ ≈ 3.414). Următoarele zerouri se află în intervalul [0, 1]. Aceste zerouri la (aproximativ) 0,586 și 0,667 (2 - √ 2 ≈ 0,586; 2/3 ≈ 0,667).

Apoi, intervalele de examinare: (-∞, -1), (-1, 0,586), (0,586, 0,667), (0,667, 3.414) și (3.414, ∞). Menționăm pe diagramă, în cazul în care funcția este negativ. Apoi, inclusiv punctele finale respective, setul de soluții este de aproximativ
[-1, 0586] [0,667, 3.414] sau.
inegalități raționale
Unele inegalități includ expresii și funcții raționale. Aceste inegalități sunt numite inegalități raționale. Pentru a le rezolva, trebuie să facem câteva ajustări la metoda anterioară.
Solve EXEMPLUL 3: (x - 3) / (x + 4) ≥ (x + 2) / (x - 5).
Soluție Mai întâi, scade (x + 2) / (x - 5) pentru a obține inegalitatea echivalentă cu 0 pe o parte:
(X - 3) / (x + 4) - (x + 2) / (x - 5) ≥ 0.
Cautam pentru toate x, pentru care caracteristica
f (x) = (x - 3) / (x + 4) - (x + 2) / (x - 5)
nedeterminat sau egal cu 0. Aceste valori sunt numite critice.
Privind la numitor, vom vedea că nu este definit pentru x = -4 și x = 5. În continuare, vom rezolva f (x) = 0:
(X - 3) / (x + 4) - (x + 2) / (x - 5) = 0.
(X + 4) (x - 5) [(x - 3) / (x + 4) - (x + 2) / (x - 5)] = (x + 4) (x - 5) .0
(X - 5) (x - 3) - (x + 4) (x + 2) = 0
(X 2 - 8x + 15) - (x 2 + 6x + 8) = 0
-14x + 7 = 0
x = 1/2.
Valori critice -4, 1/2 și 5. Se împart axa x în patru intervale:
(-∞, -4), (-4, 1/2), (1/2, 5) și (5, ∞).
Apoi folosim o valoare de test pentru a determina semnul f (x) la fiecare interval.
Valorile funcționale sunt pozitive în intervalele (- ∞, -4) și (1/2, 5). Deoarece f (1/2) = 0, iar semnul inegalității este ≥, știm că 1/2 ar trebui să fie într-o varietate de soluții. Vă rugăm să rețineți că nici -4 sau 5 nu se aplică la o varietate de f, și astfel încât acestea nu pot face parte din setul de soluție.
Decizia este stabilită (-∞ -4) [1/2, 5).
trage
y = (x - 3) / (x + 4) - (x + 2) / (x - 5).
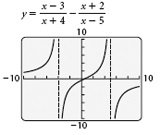
Considerăm că, la punctul 0.5 funcția este 0.
Apoi căutăm valoare, în cazul în care funcția nu este definită. Privind la numitor x + 4 și x - 5, observăm că funcția nu este definită pentru x = -4 și x = 5
Valorile critice. y unde nespecificat sau 0, este -4, 5 și 0,5.
Graficul prezinta, unde y, unde pozitive și negative. Vă rugăm să rețineți că 4 și 5 nu poate fi într-o varietate de soluții, deoarece y nu este definit pentru aceste valori. Cu toate acestea, includem 0,5, ca semn de inegalitate este ≥ și f (0,5) = 0. Setul de soluții este
(-∞, -4) [0,5, 5).
Mai jos - o metodă de rezolvare a inegalităților raționale.
Pentru rezolvarea inegalităților raționale ar trebui:
1. Găsiți inegalitatea echivalentă cu 0 pe o parte.
2. Pentru a schimba simbolul semnul inegalității pe semnul egalității și de a rezolva ecuații aferente. 3. Găsiți valorile variabilelor pentru care legate de o funcție rațională nu este definită. 4. Numerele etapele (2) și (3) sunt valorile critice. Utilizați valorile critice care împart axa orizontală în intervale. Apoi, utilizați valoarea de test x fiecărui interval pentru a determina semnul funcției în acest interval. 5. Selectați intervale pentru care inegalitatea este satisfăcută și se înregistrează valoarea intervalului. Dacă semnul inegalității este ≤ sau ≥, atunci soluția în etapa (2) trebuie să fie încorporate într-o varietate de soluții. X, găsită în etapa (3), nu sunt incluse în setul de soluție.
Acesta funcționează bine cu o combinație de metodele algebrice grafice și soluțiile polinomului inegalitățile raționale. Metode algebrice dau cifre exacte pentru valorile critice și metode grafice vă permit să vedeți cu ușurință care intervale îndeplinesc.