alte sarcini pe acest subiect
Având în vedere două vârfuri adiacente ale unui pătrat A (1, 4) și B (4, 5). Găsiți celelalte două.
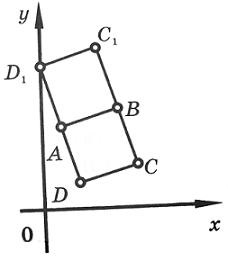
Este evident că problema admite două soluții, ca vârfuri dorite pot fi pe laturile opuse ale segmentului AB. Ecuația AB pătrat lateral va, astfel: x - 3y + 11 = 0, iar lungimea sa este. Acum, prin punctele A (1, 4) și B (4, 5) desena linii drepte perpendiculare AB. și pe fiecare dintre aceste linii este definit de cele două puncte ale căror distanță de la AB este (la pătrat toate laturile egale). Coordonatele acestor puncte și va fi căutat.
linii perpendiculare ecuația AB și care trece prin extremitățile segmentului AB. sunt după cum urmează:
Pe fiecare dintre aceste linii drepte găsi două puncte situată la o distanță de la AB egală, în care unul dintre punctele de deviere de la AB este pozitiv, la celălalt - negativ.
Să coordonatele punctului D prin x1 și y1. Din moment ce acest punct se află pe linia AD. coordonatele sale satisfac ecuatia acestei linii, adică. e. ecuație
alte sarcini pe acest subiect
Exemple de rezolvare a problemelor: date două vârfuri adiacente ale unui pătrat A (1, 4) și B (4, 5). Găsiți celelalte două.