Fig. 4.8 Proiecții con Fig. 4.9 con Izometrică
Fig. 4.5 Estimări ale cilindrului Fig. 4.6 cercul izometrică Fig. 4.7 cilindru izometrică
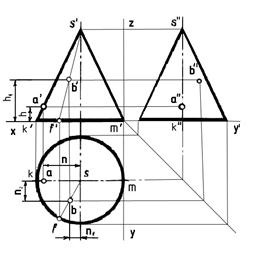
Construirea unui profil de proiecție a cilindrului:
1) y coordonatele tolerați la proiecția profilului prin intermediul liniilor de legătură cu proiecția orizontală.
2) z coordonatele bazelor inferioare și superioare tolerate prin linii de comunicație cu o proeminență frontală. Profilul de proiecție a cilindrului este o repetare a proiecției sale frontale
Construcțiile proiecții pe suprafața cilindrului:
proiecție orizontală-LARG de punctele A și B pot fi găsite prin efectuarea de puncte de date a „și b“ linii verticale datorită intersecția lor cu cercul la punctele a și b. Punct profil de proiecție A - tochkaa „“ - se bazează pe intersecția liniilor trasate din punctele și. ua“. Profil Punct de proiecție B - tochkab „“ - se bazează pe intersecția liniilor trasate din punctele. b și b“.
Izometrică înlocuit circumferința ovală. În cele două axe ovale - mari și mici. In planul hoz axa mică a ovalului este axa y în planul xy axa secundară a ovalului este axa Oz în ploskostizOu axa minoră a ovalului este axa x. Axa mare ovaluri perpendicular pe axele mici.
1) Desenați o axă mică oval (fig. 4.6).
2) efectuează o axă minoră perpendicular pe axa principală și punctul de intersecție este notat minor și a axei principale - O1 - centrul oval.
4) Din centrul O1 efectua raza cercului auxiliar egală cu raza cercului descris.
Construcție cilindru Izometrică:
1) Clădire oval - izometrie bază inferioară într-un plan orizontal (figura 4.7).
2) Din punct de ridicare cu privire la înălțimea cilindrului și a obține un punct O1. în raport cu care al doilea construct este același oval - izometrie bază superioară.
3) leagă cele două baze care formează liniile verticale.
Construcție de puncte izometrice pe suprafața cilindrului:
Izometrie punctele A și B construi în coordonatele lor luate din desenul complex (fig. 4.7).
1) Din punctul de intersecție al axei x cu baza inferioară oval amâna până la distanță h (z coordonatele punctului A), obținem punctul A.
2) trage o linie paralelă cu axa y la o distanță de ea n, obținem punctul 1.
Construcția de con de proiecție din față:
2) De la seredinyotrezka k „-m“ - amâna înălțimea conului și să construiască un punct s'- vedere frontală de sus.
Construirea unui profil de proiecție a conului:
1) y coordonatele de bază prin intermediul tolerați linii de comunicație cu o proiecție orizontală la proiecția profilului.
2) Coordonatele vârfurile conului z - litera s'- tolerat printr-o legătură de comunicație cu proiecția din față pe proiecția profilului și construcția punctului s'“.
3) con de proiecție Stroimprofilnuyu, care leagă partea de sus - punctul de s „“ - cu o bază
puncte de proiecție de construcție pe suprafețele conice:
In figura 4.8 o vedere frontală a A - tochkaa „- este pe n otrezkes'-“, prin urmare, de a construi o proiecție orizontală - litera a - este necesar să se reducă linia de comunicare din punctul a „la proiecția orizontală a acestui segment - un sn segment .Pentru a construi o proiecție profil - tochkua „“ - este necesar din punctul de „țineți legătura cu segmentul s““- 3«».
Pentru a construi un punct de proiecție B, trebuie să mergeți mai întâi printr-o vedere frontală dat - punctul în „- segmentul care leagă partea de sus la baza - s'- f“ „Apoi, găsiți proiecția orizontală a acestui segment - e - f“ și plasându-l din punct de în „link-ul, pentru a construi punct la, proiecție profil - tochkav“ „- se bazează pe intersecția liniilor trasate din punctele B și B“.
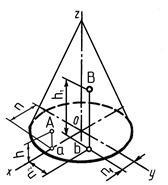
Construcția de forma conica izometrice:
1) oval Building - bază izometrie într-un plan orizontal (figura 4.9).
2) Din punct despre creșterea înălțimii conului și a obține punctul de s - partea de sus a conului.
3) Desenați două linii generatoare de sus în jos.
Construcție de puncte izometrice pe suprafața conului;
Izometrie punctele A și B construi în coordonatele lor luate din desenul complex (fig. 4.9).