electrostatică
Exemple de rezolvare a problemelor
W
Având în vedere prin: m1 = m2 = m = kg - mingi de masă, distanța dintre bile, - unghiul format de fire, constanta dielectrică, Kd - sarcina unui electron.
Găsiți: Q- încărcarea inițială a mingii; n - numărul de electroni în exces pe fiecare bec.
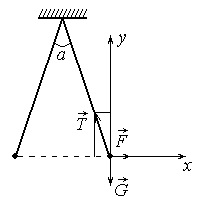
Decizie. Ca și în problema nu este menționat mediu se presupune că taxele interacționează în vid. Conform legii de conservare a taxa în bile de contact pe fiecare dintre ele va taxa q / 2. bilele sunt trei forțe: forța gravitațională G = mg. fir de reacție T forță de tracțiune, puterea interacțiunii electrice
În cazul soldului suma algebrică a proiecțiilor acestor forțe pe direcție verticală și orizontală este egală cu zero:
T · cos (α / 2) - mg = 0, F - T · sin (α / 2) = 0
Rezolvarea sistemului de ecuații pentru F. primi:
Substituind valoarea F de formula legii lui Coulomb, obținem o expresie pentru sarcină q.
Având în vedere că fiecare minge a fost încărcat, defini n =.
Substituind date numerice, obținem
Am găsit numărul de electroni în exces pe fiecare bec:
A: taxa inițială mingea este egală cu 7,3 · 10 CI; numărul de electroni în exces pe fiecare bec aproximativ 4,6 · 10.
Sarcină. Placă condensator, suprafața fiecărei plăci este de 6,2 x 10 -3 m 2 umplută cu mică constantă dielectrică relativă 6. Distanța dintre plăcile de 2,00 mm. Se determină capacitatea electrică a condensatorului, diferența de potențial între plăcile sale, intensitatea câmpului într-un condensator și forța de atracție reciprocă a plăcilor în cazul în care taxa pe fiecare dintre ele este egal cu 4,00 × 10 -8 kD.
Acesta este dat de: S = 6,2 · 10 -3 m 2 - o zonă placă, d = 2,00 · 10 -3 m - distanța dintre plăci, ε ε = 6 - constanta relativa dielectrică a mediului, q = 10 · 4,00 Cl -8 - taxa pe o farfurie, ε0 = 8,85 · 10 -12 F / m - constanta electric.
Găsiți: C - capacitatea electrică a condensatorului; U - diferența de potențial pe plăci; E - intensitatea câmpului într-un condensator; F - forța plăcilor de atracție reciproce.
Decizie. capacitanță electrică a condensatorului este definit prin condensator plat formulă capacitate:
Cunoașterea sarcină q și capacitatea C definesc diferența de potențial între plăcile condensatorului:
Intensitatea câmpului în interiorul condensatorului și diferența de potențial între plăcile sale legate de relația
Deoarece câmpul dintre plăcile se obține prin suprapunerea celor două domenii (ambele plăci) o placă de câmp putere E „= E / 2. Forța cu care fiecare dintre plăcile atrage o alta,
Folosind datele numerice din condițiile înregistrate ale problemei și a formula, vom determina cantitățile necunoscute:
Răspuns. capacitanță condensator electric 1,65 · 10 -10 F; diferența de potențial pe plăcile 242; Intensitatea câmpului în condensatoare 1,21 · 10 5 V / m; forța plăcilor de atracție reciproce 2,42 ·· 10 -3 N.
Sarcină. Se determină capacitatea electrică a condensatorului, care este utilizat pentru fabricarea aluminiului folie de lungime de 157 cm și o lățime de 90,0 mm. hârtie cerată grosime 0,10 mm. Ce energie este stocată în condensator, atunci când acesta este încărcat la tensiunea de funcționare de 4,0 × 10 2?
Dată de: l = 157 cm = 1,57 m - lungimea de folie de aluminiu, h = 90,0 mm = 9,0 x 10 -2 m - lățime folie, d = 0,10 mm = 0,10 x 10 -3 m - grosimea hârtiei cerate, U = 4,0 · 10 B februarie - tensiune pe plăcile condensatorului, - constanta dielectrică, ε = 2,0 - permitivitate relativă de hârtie cerată.
Găsiți: C - capacitatea electrică a condensatorului, W - condensator de energie.
Decizie. Pentru a găsi capacitatea electrică folosind formula
energia condensatorului calculat prin formula
Folosind datele numerice ale condițiilor problemei, vom găsi
Răspuns. capacitanță electrică a condensatorului 25 microfarazi · 10 -3; energia condensatorului 2 mJ.
Sarcină. Trei condensator cu capacitate C1 = 0,2 microfarazi C2 = C3 = 0.4 microfarazi conectate conform schemei prezentate în figură și sunt conectate la o sursă de curent continuu de tensiune UAV = 250 B. Găsiți tariful total, taxele și diferența de potențial a lungul condensatoarelor individuale. Determinarea condensatoarele bateriei de stocare de energie electrică.
Având în vedere: C1 = 0,2 x 10 -6 F, C 2 = C 3 = 0,4 x 10 -6 F - electrice condensatorii de capacitate = 250 UAV - tensiune aplicată la condensatori.
Găsiți: q, q1, q2, q3 - taxa totală și taxa pe condensator; U1, U2, U3 - diferența de potențial peste plăcile de condensatoare, W - energia electrică stocată de toate condensatori.
Decizie. taxa globală necunoscută este determinată de formula
unde C - capacitatea electrică a condensatorului (baterie) - se amestecă prin formula de conexiuni (paralele și seriale):
Taxa primului condensator este aceeași ca taxa totală:
și taxele pe celelalte două condensatoare
q2 = q3 = q / 2.
Cunoscând capacitatea și taxa fiecărui condensator, putem găsi diferența de potențial pe farfuriile lor.
Pentru a găsi energia stocată de o baterie de condensatoare, se folosește formula
Gasim stocate de încărcare a bateriei:
taxele pe condensatoarele individuale:
Calculăm diferența de potențial și energia totală:
Răspuns. Sarcina bateriei și primul condensator, al doilea condensator și al treilea - pe; diferența de potențial: 200.50 și 50B; energia totală.