Una dintre metodele de rezolvare a problemelor în construirea unei metode de loci.
Locus de puncte se numește o cifră care constă din toate punctele în plan, au anumite proprietăți.
De exemplu, un cerc poate fi definit ca locul geometric al punctelor echidistante dintr-un anumit punct.
Un locus important al punctelor de date de următoarea teoremă:
Locul geometric al punctelor echidistant față de cele două puncte de date este o linie dreaptă perpendicular pe segmentul de linie care leagă aceste puncte și trece prin mijlocul acesteia.
Dovada. Fie A și B - punctul de date, și - o linie care trece prin centrul O al segmentului AB perpendicular pe acestea (figura 105.). Noi trebuie să dovedească faptul că:
1) fiecare punct al liniei și echidistant față de punctele A și B;
2) fiecare punct D plan echidistant față de punctele A la B, și se află pe linia.
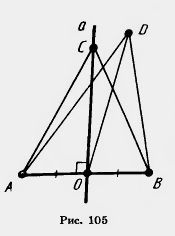
Faptul că fiecare linie și punct drepte C este echidistant față de punctele A și B, din egalitatea triunghiurilor BOC și AOC. In aceste triunghiuri unghiurile în partea de sus pe partea directă, funcționare totală, și AO = OB, deoarece G - punctul median al AB.
acum ne arată că fiecare punct D plan echidistant față de punctele A și B, și se află pe linia. Luați în considerare triunghiul ADB. El isoscel, deoarece AD = BD. Acesta DO - mediană. Prin proprietatea unui triunghi isoscel mediana tras la baza este mare. Prin urmare, punctul D se află pe o linie dreaptă. Acest lucru dovedește teorema.
A. V. Pogorelov, Geometrie pentru clasele 7-11, manual pentru instituțiile de învățământ
Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.
Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.