f (x) = a n x n + a n # X2212; 1 x n # X2212; 1 + # X22EF; + A 2 x 2 + 1 x + o 0 = # X2211; i = 0 n o i x i x ^ + a_x ^ + \ dotsb + a_x ^ + a_x + o _ = \ sum _ ^ a_x ^>.
în cazul în care n # X2208; N>. a n. a n # X2212; 1. # X2026;. a 2. 1. a a 0 # X2208; R, o _, \ ldots, a_, a_, a_ \ în \ mathbb> și n # X2260; 0 \ neq 0>. Un caz special a funcției raționale integral este o funcție f (x) = 0. toți coeficienții sunt zero. Funcția rațională completă este o combinație liniară a mai multor funcții exponențiale, și (împreună cu funcția rațională) este un caz special de funcții raționale. Cele mai simple reprezentanți ai unei întregi funcții raționale este o constantă. Funcții liniare și pătratice.
Concepte de bază [| ]
Terminologie [| ]
Therm înregistrare funcție polinomială este un polinom într-o singură variabilă. Numărul n natural (cel mai mare exponent variabil x) determină gradul funcției polinomiale. Numărul real al unui n. # X2026;. un 2. 1. 0, \ ldots, a_, a_, a_> numit coeficienții funcției polinomiale. Numărul unui n> adesea numit cel mai important coeficient, și un> număr 0 - raportul liber.
Cazuri speciale [| ]
Exemple [| ]
Proprietăți de bază [| ]
Domeniul unui set de valori, dincolo de [| ]
Funcția polinomială peste câmpul numerelor reale este definită peste tot și este continuă pe tot domeniul său. Acesta valori stabilite, de asemenea este un subset al setului de numere reale. Pentru chiar valori ale lui n este setat, în funcție de semnul coeficientului de conducere a n>. limitată la partea de sus sau de jos (a se vedea. De asemenea, tabelul).
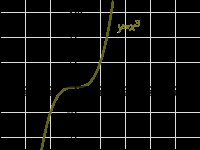
Limita unei funcții polinomiale de x la infinit # X2192; # X00B1; # X221E; întotdeauna există, iar valoarea sa specifică depinde de n semnul planeitate și gradul de coeficientul de conducere a n>. In acest grafic funcție polinomială se comportă exact ca un program și o funcție de putere g (x) = a n x n x ^>:
polinomială este diferențiabilă pe tot domeniul său. derivatul său este ușor de găsit de reguli elementare de derivare. Astfel, derivata funcției f (x) = 2 x 3 # X2212; 4 x 2 x 5 + # X2212; 1 -4x ^ + 5x-1> se calculează după cum urmează:
f # X2032; (X) = (2 x 3 # X2212; 4 x 2 x 5 + # X2212; 1) # X2032; = (2 x 3) # X2032; + ( # X2212; 4 x 2) # X2032; + (5 x) # X2032; + ( # X2212; 1) # X2032; = 2 # X22C5; 3 x 2 # X2212; 4 # X22C5; 2 x + 5 # X22C5; 1 x 0 # X2212; 1 # X22C5; 0 = 6 x 2 # X2212; 8 5 x + f '(x) = (2x ^ ^ + -4x-5x 1)' \\ = (2x ^) '+ (- 4x ^)' + (5x) '+ (- 1)' \\ = 2 \ cdot 3x ^ -4 \ cdot 2x + 5 \ cdot 1x ^ -1 \ cdot 0 \\ = 6x ^ -8x + 5 \ end >>
Funcția polinomială este, de asemenea, integrabil în toate domeniul său de aplicare. primitiv ei este, de asemenea, ușor cu ajutorul regulilor elementare de integrare. De exemplu, aceeași primitivă funcția f (x). ca în exemplul de mai sus, se calculează după cum urmează:
Este ușor de văzut că derivatul și pervobraznaya funcție polinomială f (x) de grad n și sunt ele însele polinomială. În acest caz, funcția f # X2032; (X) este de gradul n # X2212; 1 și funcția F (x) - gradul n + 1 (cu excepția cazului în care trivială f (x) = 0).
Condiții speciale ale funcției polinomiale [| ]
Calculul de zerouri [| ]
Zerourile unei funcții polinomiale coincid cu rădăcinile polinomului. prezent în ecuația lui. Astfel, pentru a găsi zerouri nevoie pentru a rezolva ecuatia f (x) = 0. Metoda de soluție depinde de funcția specifică a ecuației.
Dacă funcția f (x) = a n x n + # X22EF; + A 2 x 2 + 1 x + o 0 x ^ + \ dotsb + a_x ^ + a_x + a_> to factor de scris in forma f (x) = a n # X22C5; (x # X2212; x 1) k 1 # X22C5; (x # X2212; x 2) k 2 # X22EF; (x # X2212; x m) k m \ cdot (x-x _) ^> \ cdot (x-x _) ^> \ dotsb (x-x _) ^ >>. în care fiecare factor reprezintă un binom liniar. numerele reale x 1>. x 2>. ..., x m> sunt zero ale funcției f (x). iar numerele k 1>. k 2>. ..., k m> arată multiplicitatea zerourilor corespunzătoare acestei funcții. În acest caz, condiția: k 1 + 2 + K # X22EF; + K m # X2264; n + K + _ \ dotsb + k_ \ n Leq>. Astfel, gradul n funcția f (x) determină numărul maxim posibil de zerouri peste câmpul numerelor reale. În cazul în care o generalizare a funcției polinomiale în domeniul numerelor complexe. în conformitate cu teorema fundamentală a algebrei. are loc egalitate: 1 K + K 2 + # X22EF; + K m = n + k _ + \ dotsb + k_ = n>.
De exemplu, o funcție polinomială f (x) = # X2212; 0. 01 # X22C5; x 3 # X22C5; (x # X2212; 2) # X22C5; (X + 3) 2 # X22C5; (X 2 + 1) 01 \ cdot x ^ \ cdot (x-2) \ cdot (x + 3) ^ \ cdot (x ^ + 1)> are trei zerouri, și anume: x 1 = 0 = 0> ( multiplicitate 3), x 2 = 2 2 => (multiplicitate 1) și x = 3 # X2212; 3 = -3> (de 2 ori). pătrat binom x 2 + 1 + 1> nu are rădăcini reale, deci nu poate fi în continuare factor în factori liniari.
În general, pentru a găsi zerourile o funcție polinomială de gradul n = 1 și n = 2, folosind tehnici care sunt utilizate pentru soluțiile, respectiv ecuațiile liniare și pătratice. Pentru a găsi zerourile o funcție polinom de gradul n # X2265; 3 în cazul în care acesta poate fi utilizat diferite metode de soluții speciale de ecuații algebrice de grad superior (în special în ceea ce privește puterea și ecuațiile biquadratic). În mai multe cazuri generale se aplică orice astfel de tehnici universale, cum ar fi polinomială diviziune lungă sau schema Horner. permițând totuși găsită numai întreg (exact) se folosesc soluții sau metode numerice (de exemplu, metoda lui Newton) pentru găsirea tuturor soluțiilor (dar numai aproximative).

Metode de a găsi rădăcinile întregi ale polinomului bazate pe investigarea teoremei Bézout. În particular, coeficientul polinom funcția f (x) = a n x n + # X22EF; + A 2 x 2 + 1 x + o 0 x ^ + \ dotsb + a_x ^ + a_x + a_> cu coeficienți întregi inițial între toate divizorii coeficient liber un 0> este selectat oricare rădăcină x 0>. care este un număr întreg, pentru care deține: f (x 0) = 0) = 0>. Apoi, prin împărțirea coloanei sau prin schema Horner polinom f (x) la x binomial # X2212; x 0> făcut la forma f polinomului original (x) = factorizare (x # X2212; x 0) # X22C5; g (x)) \ cdot g (x)>. unde g (x) - un polinom de gradul n # X2212; 1. Astfel, gradul de funcția originală, și, prin urmare, complexitatea acestuia este redusă. Găsirea zerourilor f (x) se reduce la găsirea zerourile funcția g (x).
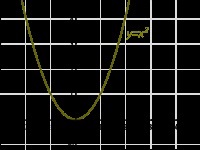
De exemplu, pentru a găsi zerourile funcției f (x) = x 3 # X2212; 12 x 2 + x 5 + 150 -12x ^ + 5x + 150> (vezi. Exemplu) cu coeficienți întregi primul "ghici" unul rădăcină (numărul 5 este printre divizori de 150), apoi f polinomul original (x) este împărțit în x binomice # X2212; 5. O constatare suplimentară a restului zerouri f (x) se reduce la găsirea zerourile funcției rezultată g (x) = x 2 # X2212; 7 x # X2212; 30 -7x-30>. care poate fi ușor de găsit prin rezolvarea ecuației pătratice corespunzătoare.
Monotonie și punctul extremum [| ]