18.1. Găsiți numărul tuturor:
a) numere din două cifre;
b) numere din două cifre, care constau din diferite cifre;
c) numere din două cifre, suma de cifre este mai mare de 16;
g) numere din două cifre, din care produsul este mai mic de 2 cifre.
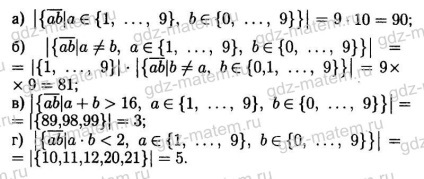
18.2. Din figurile 4, 6, 7 cuprind diverse numere cu trei cifre fără a repeta cifre.
a) Găsiți cel mai mare număr.
b) Găsiți cel mai mic număr al cărui cifre doilea este 7.
c) Câte numere se termină în figura 7, poate fi co-pariu?
g) Câte numere pot fi formate?
18.3. Din cifrele 0, 1, 4, 8, 9 reprezintă un număr din două cifre (numere de repetiție permis).
a) Găsiți cel mai mare număr.
b) Găsiți cel mai mic număr care este divizibil cu 9.
c) Câte numere chiar și pot fi formate?
g) Enumera toate numerele care sunt multipli de 8.
18.4. Micul dejun pe o bucată de pâine albă, neagră sau de secară pot fi puse brânză sau cârnați. Sandwich pot fi spălate în jos cu ceai, lapte sau iaurt.
a) Desenați un arbore de opțiuni posibile pentru micul dejun.
b) pentru băuturi din lapte vor fi selectate în modul în multe cazuri?
c) Care este mai probabil: că pâinea de secară este, sau ce se va întâmpla cu brânză sandwich?
d) Cum va arborele de opțiuni, dacă știți că brânza este pus pe pâine neagră și cârnați nu va bea chefir?
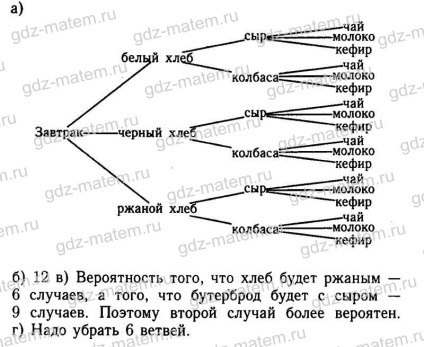
18.5. O urnă mint nouă pot fi distinse cu bile la atingere: cinci alb și negru patru. Scoate două bile simultan. Dacă acestea sunt de diferite culori, acestea sunt retrase din circuitul agricol, iar în cazul în care aceeași culoare, apoi a revenit la urnă. Această operație se repetă de două ori.
a) Desenați o serie de opțiuni de copac.
b) În câte cazuri va fi de nouă bile într-o urnă?
c) În câte cazuri în urnă va fi nu mai mult de cinci mingi?
g) Desenați un arbore de opțiuni posibile în cazul în care condiția specificată în operația se repetă de trei ori.
18.6. În hol sunt trei becuri.
a) Câte diferite moduri de iluminare a coridorului, inclusiv în cazul în care toate luminile sunt stinse?
b) Cât de multe moduri de iluminare diferite, dacă știți că numărul de becuri 1 și numărul 2 sunt aprinse sau nu aprinse în același timp?
c) Cât de multe moduri de iluminare diferite, în cazul în care se știe că la arderea de lumină bec număr lampă 3 numărul 2 nu se aprinde?
g) Cât de multe moduri diferite de iluminare a coridorului, atunci când este aprins, cele mai multe becuri?

18.7. Mai multe țări au decis să utilizeze dreptunghi național de pavilion împărțit în patru benzi verticale de lățime egală în diferite culori: alb, albastru, roșu, verde. În fiecare țară - pavilionul său. Cât de multe țări:
a) se pot utiliza astfel de steaguri;
b) se pot utiliza semnalizatoare cu prima bandă albă;
c) pot fi utilizate cu steaguri terțe sunt benzi nu verde;
g) poate fi utilizat cu un steaguri albastre cu dungi roșii aranjate într-un rând?

18.8. Cartea de colorat disjuncte trase triunghi, pătrat și cerc. Fiecare cifră ar trebui să fie vopsea într-una dintre culorile curcubeului, cifre diferite - în culori diferite.
a) Cât de multe moduri sunt acolo pentru pictura?
b) Cât de mulți dintre ei sunt cei care cerc - Orange?
c) Câte dintre ele sunt cele în care triunghiul - nu roșu?
g) Cât de multe moduri sunt acolo pentru a fi colorate în culori reci?

18,9. Pe plan de coordonate marcat toate punctele, abscisa și ordonata, care sunt una dintre următoarele numere: -3, -1, 1, 2, 7 (repetarea permis).
a) Câte dintre aceste puncte?
b) Câte puncte se află în stânga axei y?
c) Câte puncte este mai mare decât axa x?
g) Câte puncte se află într-un cerc cu raza de 5 cu centrul la origine?

18.10. Este cunoscut faptul că x = 2a3b5s și a, b, c - numărul pluralității (coincidență permisă).
a) Găsiți valorile maxime ale x și minime.
b) Câte dintre aceste numere pot fi formate?
c) Cât de mulți dintre ei vor chiar numere?
g) Câte dintre aceste numere va fi reziliat nul?

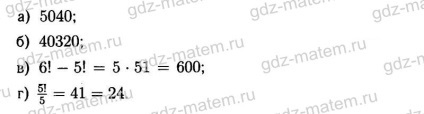

18.13. Este împărțit 11! pe:
a) 64; b) 25; c) 81; d) 49?

18.15. Rezolva în numere întregi pozitive ecuația:
! A) n = 7 (n - 1)!; c) (k - 10)! 77 = (k - 11)!;
b) (m + 17)! = 420 (m + 15)!; g) (3x)! = 504 (3x - 3)!.

18.16. oaspeții au sosit A, B, C, D. Masa rotundă la proprietarul casei - cinci scaune diferite.
a) Cât de multe moduri sunt acolo de locuri?
b) Câte sunt modalitățile de ședere în cazul în care locul este deja cunoscut maestru al casei?
c) Câte sunt modalitățile de ședere, dacă știți că oaspeții cu ar trebui să pună de lângă invitatul lui A?
g) Cât de multe moduri sunt acolo de locuri, dacă știm că un invitat nu ar trebui să fie plantați în apropierea oaspetele de D?

18.17. Din cifrele 0, 2, 8, 9 reprezintă diferite numere de trei cifre (numere permise de repetiție).
a) Găsiți cel mai mic număr.
b) Introduceți toate numerele care sunt mai mici de 250.
c) Identificarea orice număr impar mai mare de 900.
d) lista toate numerele care sunt multipli de 40.
18.18. În partea de jos a portofoliului sunt imperceptibile pentru stilouri tactile: două simple și trei culori. Elev îi scoate unul câte unul. Are nevoie de creioane colorate și un creion excavat trimite înapoi la partea de jos a portofoliului, și frunze colorate pe masă. Această operație se repetă de trei ori.
a) Desenați o serie de opțiuni de copac.
b) În câte cazuri, toate creioane stabilite va fi simplu?
c) În câte cazuri, toate prevăzute creioane colorate sunt?
d) În câte cazuri, printre creioane colorate stabilite pentru a fi mai mult decât simplu?
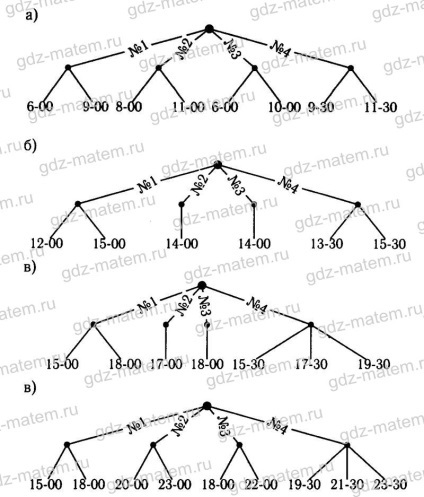
18.19. Tabelul de mai jos conține informații despre producția de știri în patru canale de televiziune.
Vrei să alegeți un comunicat de presă. Desenează un arbore de opțiuni posibile pentru perioada:
a) de la 11-45 la 6-00; c) de la 15-00 la 19-45;
b) 12-00 la 15-45; d) 18-00 la 23-45.
18.20. Cadru didactic se pregătească pentru teste patru probleme pentru a rezolva inegalitățile liniare, cinci probleme de cuvânt (două pe mișcare și trei la locul de muncă) și șase sarcini pentru soluția ecuațiilor pătratice (două sarcini discriminant este negativ). Controlul ar trebui să fie o problemă pentru fiecare dintre cele trei subiecte. Găsiți numărul total de:
a) toate opțiunile de control posibile;
b) acele opțiuni, care se vor întâlni problema privind mișcarea;
c) acele opțiuni, care au o ecuație pătratică este cel puțin o rădăcină;
g) acele opțiuni care nu îndeplinesc în același timp, sarcina de a lucra și ecuația de gradul doi care nu are rădăcini.
18.21. Controlul va avea cinci sarcini: una dintre cele cinci teme trecut. Pentru fiecare subiect, profesorul a făcut o listă cu zece sarcini. Este cunoscut faptul că, controlul va fi provocări din aceste liste. Pentru fiecare subiect, elevul este capabil să rezolve opt probleme și nu este în măsură să rezolve două probleme. Caută:
a) numărul total al tuturor opțiunilor de control;
b) numărul de opțiuni în care elevul este capabil să rezolve toate cele cinci obiective;
c) numărul de opțiuni în care studentul nu rezolvă nici o problemă;
g) numărul de opțiuni în care elevul este capabil să rezolve toate problemele, cu excepția primei.
18,22. Este cunoscut faptul că x = 2aZb5s și a, b, c - numărul de seturi diferite.
a) Găsiți valorile maxime ale x și minime.
b) Câte dintre aceste numere pot fi formate?
c) Cât de mulți dintre ei vor fi numere impare?
g) Cât de mulți dintre ei vor fi multipli de 12?
18.23. a) punctele (0, 0), (2, 0), (3, 2) sunt noduri ale triunghiului. Cât de multe moduri pot fi desemnate în partea de sus a literele A, B, C?
b) punctele (0, 0), (0, 4), (3, 0), (3, 7) sunt nodurile unui trapez. Cât de multe moduri pot fi desemnate în partea de sus a literelor K, L, M, N?
c) Punctele (1, -3), (0, 0), (0, 4), (3, 0), (3, 7) sunt noduri ale unui convex pentagon. Cât de multe moduri de a defini aceste vârfuri literele P, R, S, T, Q?
d) În câte cazuri în loc de muncă în) de PR este una dintre părți?
18.24. Echipa de volei a șase persoane, iar la locul de șase poziții (numere) pentru plasarea acestora.
a) În câte feluri echipa poate rămâne pe site?
b) Câte feluri există locuri în care căpitanul este pe teren?
c) Cât de multe moduri de aranjament în care căpitanul nu se află pe teren?
g) Câte feluri există locuri în care căpitanul este fie pe teren sau pe site-ul unui punct de pază?
18.25. Simplificați expresia:
