3. Structurile ciclice ale Programului
Calculează suma unei serii infinite de o anumită precizie
Având în vedere o secvență de numere R1. R2. R3, ..., Rn, .... Expresia R1 + R2 + R3 + ... + Rn + ... nazyvayutbeskonechnym următor. sau prostoryadom. și numărul R1. R2. R3, ... Statele membre ale seriei. În acest caz, ține cont de faptul că suma seriei începe cu acumularea primelor membri. Suma Sn =

Acesta este seria convergentă. în cazul în care secvența de sume parțiale are o limită iraskhodyaschimsya - în caz contrar. Conceptul de suma unui număr poate fi extins [9], iar apoi unele serii divergente vor avea, de asemenea, sume. Imennorasshirennoeponimaniesummyryada vor fi utilizate în dezvoltarea algoritmilor pentru următoarea problemă: acumularea sumelor trebuie efectuate atâta timp cât un membru obișnuit al unui număr de valoare absolută mai mare decât o valoare predeterminată ε.
În general, toate sau o parte din termenii seriei pot fi specificate expresii, care depind de numărul de numărul de membri și variabile. De exemplu,
Se pune întrebarea pentru a minimiza cantitatea de calcul - se calculează valoarea următorului termen al seriei de formula generală a unui număr de membri (în exemplul de mai sus, este o expresie a sumei) cu formula recurență (output-l este prezentată mai jos), sau de a folosi o formulă de recurență numai pentru exprimarea unui număr de unități membre (cm. mai jos).
Concluzie formulă de recurență pentru calcularea numărului de membri
Să presupunem că doriți să găsiți o serie de numere R1. R2. R3, ..., secvențial calcularea acestora în conformitate cu formulele

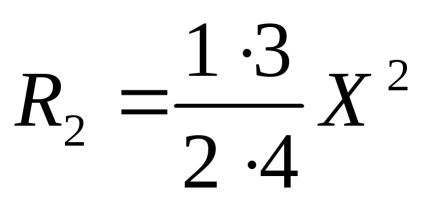
Pentru a reduce calculul în acest caz, este convenabil să se folosească rekurrentnoyformuloy natură, care permite să se calculeze valoarea RN pentru N> 1, cunoscând valoarea membrului anterior al unui număr de RN-1. unde


Astfel, formula recursie devine.
Dintr-o comparație a numărului total de membri cu formula (3.1) și recurente (3.2), care simplifică foarte mult calcularea formulei recurență. Este aplicabil pentru N = 2, 3 și 4 știu că

Metoda de calcul a valorii unui număr de membru
Pentru a calcula valorile termenilor seriei, în funcție de tipul acestuia, poate fi preferabil să se utilizeze un membru al unui număr de formula generală sau o formulă de recurență sau o metodă mixtă de calcul a valorilor unui număr de membri. atunci când una sau mai multe dintr-un număr de porțiuni membre sunt utilizate formule de recurență, atunci valorile lor sunt substituite în elementul formula generală serie. De exemplu, - ryadaprosche pentru a calcula valoarea unui număr de membru








Exemplu 3.2.1 căutare
Se calculează cu precizie ε 0 pentru o X45 o
valorile aproximative ale cos X în conformitate cu formula:
folosind o formulă recursiv pentru calcularea numărului de membri:

valoarea exactă a funcției cos X,
eroarea absolută și relativă a valorilor aproximative.